Les fractions sont une manière de représenter la quantité que l’on prend d’un objet divisé en plusieurs morceaux. La valeur représentée par une fraction peut être plus petite que 1, égale à 1 ou plus grande que 1.
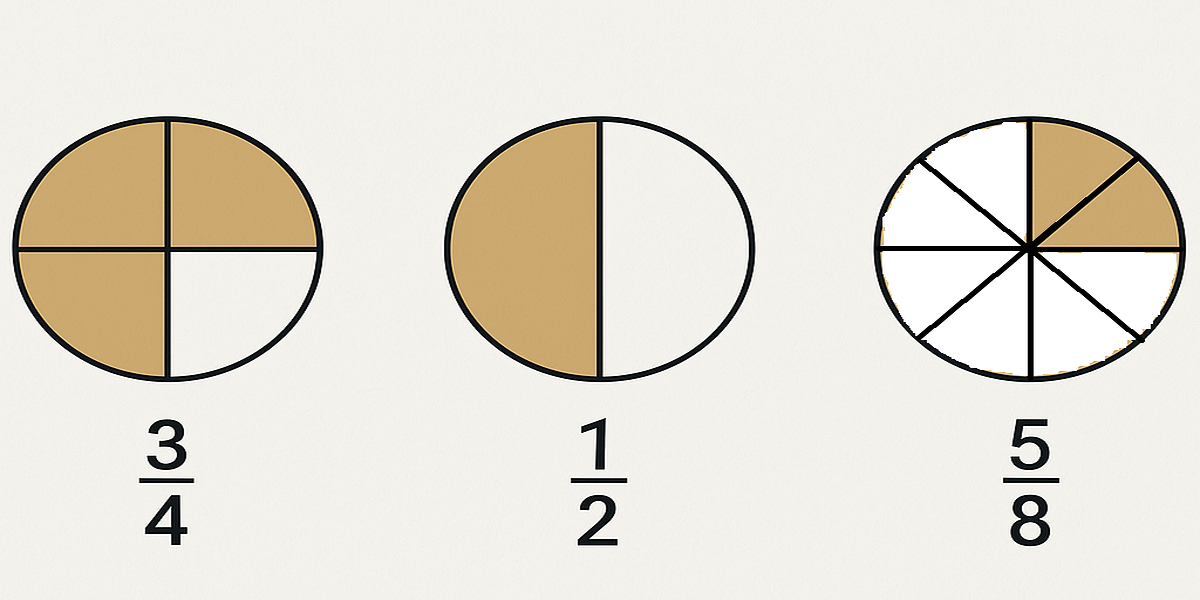
Une fraction est composée de deux nombres:
- Le numérateur (celui qui est en haut) indique combien de partie qu’on prend.
- Le dénominateur (celui qui est en bas) indique en combien de partie l’objet est séparé.
NB. Le dénominateur d’une fraction ne peut jamais être zéro, parce qu’on ne peut pas partager zéro.
Une fraction est plus grande que 1 (l’unité) si le numérateur est plus grand que le dénominateur.
$$Exemple: \frac{3}{2}; \frac{4}{2}; \frac{5}{3}; \frac{28}{4}; \frac{11}{10}\ et\ d'autres.$$Une fraction est égale à 1 (l’unité) si le numérateur est égale au dénominateur.
$$Exemple:\frac{1}{1}; \frac{2}{2}; \frac{3}{3}; \frac{4}{4}; \frac{5}{5};\ ainsi\ de\ suite.$$Une fraction est plus petite que 1 (l’unité) si le numérateur est plus petit que le dénominateur.
$$Exemple: \frac{1}{4}; \frac{4}{6}; \frac{3}{9}; \frac{5}{7}; \frac{8}{11}; ainsi\ de\ suite.$$Deux fractions sont équivalentes (ou égales) si lorsque l’on multiplie (ou divise) numérateur et dénominateur d’une fraction par le même nombre non nul, on obtient l’autre fraction
$$Exemple: \frac{1}{2}; \frac{2}{4}; \frac{3}{6}; \frac{4}{8}; \frac{5}{10}\ sont\ des\ fractions\ équivalentes$$$$\frac{1×2}{2×2}= \frac{2}{4}; \frac{1×3}{2×3}= \frac{3}{6}$$$$\frac{1×4}{2×4}= \frac{4}{8}; \frac{1×5}{2×5}= \frac{5}{10}$$$$\frac{5÷5}{10÷5}= \frac{1}{2}; \frac{4÷4}{8÷4}= \frac{1}{2}$$Si on divise leur numérateur par leur dénominateur, elles donnent le même résultat.
1÷2= 0,5; 2÷4= 0,5; 3÷6= 0,5; 4÷8= 0,5; 5÷10= 0,5.
Lecture et Opérations des fractions
$$\frac{3}{4}\ se\ lit: trois\ quart;$$$$\frac{5}{8}\ se\ lit: cinq\ huitième;$$$$\frac{2}{2}\ se\ lit: deux\ demi;$$$$\frac{3}{6}\ se\ lit: trois\ sixième.$$$$\frac{3}{4}+\frac{5}{8}=> \frac{6}{8}+\frac{5}{8}= \frac{11}{8} = 1\frac{3}{8}$$$$\frac{2}{2}-\frac{3}{6}=>\frac{6}{6}-\frac{3}{6}= \frac{3}{6} = \frac{1}{2}$$$$\frac{3}{4}×\frac{2}{2}=> \frac{3×2}{4×2}= \frac{6}{8}$$$$\frac{2}{2}÷\frac{3}{6}=> \frac{2}{2}×\frac{6}{3}= \frac{12}{6}= 2$$Additioner les fractions
Soustraire les fractions
Multiplier les fractions
Diviser les fractions
Additioner les fractions
Pour additionner deux fractions, on doit les mettre sur même dénominateur et ensuite on additionne le numérateur de la première fraction avec le numérateur de la deuxième; puis, on conserve le dénominateur commun.
Voir: Les Plus Petits Multiples Commun
$$Exemple: \frac{3}{5}+\frac{1}{6}=>$$Pour commencer, on doit les mettre d’abord sur même dénominateur, le dénominateur commun entre 5 et 6 est: 30; maintenent pour trouver le numérateur, divisez le dénominateur commun par l’autre dénominateur, puis multipliez le résultat par le numérateur; d’où: 30÷5= 6; 6×3=18 et 30÷6= 5; 5×1= 5.
$$a) \frac{3}{5}+\frac{1}{6}= \frac{18}{30}+\frac{5}{30}=\frac{23}{30}$$$$b) \frac{4}{3}+\frac{2}{5}+\frac{7}{2}=>$$Le dénominateur commun pour 3, 5, 2 est 30.
$$\frac{4}{3}+\frac{2}{5}+\frac{7}{2}=> \frac{40}{30}+\frac{12}{30}+\frac{105}{30}= \frac{157}{30}$$Quand le résultat donne une fraction ayant le numérateur plus grand le dénominateur, divisez le numérateur par le dénominateur pour trouver le nombre entier puis l’autre fraction.
Divisons le numérateur par le dénominateur: 157÷30= 5 et reste 7;
$$D'où: 5\frac{7}{30}$$$$c) \frac{2}{3}+\frac{4}{5}+\frac{7}{9}=> \frac{30}{45}+\frac{36}{45}+\frac{35}{45}= \frac{101}{45}=> 2\frac{11}{45}$$$$d) \frac{2}{3}+\frac{1}{6}=> \frac{4}{6}+\frac{1}{6}= \frac{5}{6}$$$$e) 4+3\frac{1}{2}+6\frac{1}{2}=>$$Additionnez les entiers entre eux, et effectuez les fractions.
$$13\frac{1}{2}+\frac{1}{2}= 13\frac{2}{2}=> 13+1= 14$$$$f) 25\frac{1}{3}+3\frac{1}{4}+4\frac{5}{6}=>$$$$32\frac{4+3+10}{12}=\frac{17}{12} => 1\frac{5}{12}$$Soustraire les fractions
Pour soustraire deux fractions, on doit les mettre sur même dénominateur et ensuite on soustrait le numérateur de la première fraction avec le numérateur de la deuxième; puis, on conserve le dénominateur commun.
Exemple:
$$a) \frac{5}{8}-\frac{3}{8}= \frac{2}{8}$$$$b) \frac{7}{5}-\frac{2}{5}= \frac{5}{5}= 1$$Mettez ces fractions sur même dénominateur et soustrayez-les.
$$c) \frac{6}{7}-\frac{3}{4}=>$$$$\frac{6}{7}-\frac{3}{4}=> \frac{24}{28}-\frac{21}{28}= \frac{3}{28}$$$$d) 2-\frac{1}{3}=>$$$$2-\frac{1}{3}=> \frac{6}{3}-\frac{1}{3}= \frac{5}{3}=> 1\frac{1}{3}$$$$e) 9-1\frac{9}{10}=> 9-\frac{19}{10}=>$$$$\frac{90}{10}-\frac{19}{10}= \frac{71}{10}=> 7\frac{1}{10}$$$$f) 3\frac{2}{3}-1\frac{1}{2}=> 2\frac{4-3}{6}= 2\frac{1}{6}$$Multiplier les fractions
Pour multiplier deux fractions, on multiplie le numérateur de l’une par le numérateur de l’autre et on multiplie le dénominateur de l’une par le dénominateur de l’autre.
Exemple:
$$a) \frac{5}{7}×\frac{1}{2}= \frac{5}{14}$$$$b) \frac{2}{3}×\frac{8}{9}= \frac{16}{27}$$$$c) \frac{1}{2}×\frac{2}{3}×\frac{3}{4}= \frac{6}{24}$$$$d) 7\frac{1}{2}×3=>$$Les nombres sont considérés comme des fractions ayant 1 comme dénominateur, comme si on a: 7 sur 1 multiplié par 1 sur 2 multiplié par 3 sur 1.
$$\frac{7×1×3}{1×2×1}= \frac{21}{2}=> 10\frac{1}{2}$$$$e) 7×3\frac{3}{4}=> \frac{7×3×3}{4}= \frac{63}{4}=> 15\frac{3}{4}$$$$f) 7\frac{1}{5}×2\frac{3}{4}=> \frac{7×1×2×3}{5×4}= \frac{42}{20}=> 2\frac{2}{20}$$Diviser les fractions
Pour diviser une fraction par une autre, on multiplie la première par la deuxième inversée.
Exemple:
$$a) \frac{12}{3}÷\frac{4}{2}=> \frac{12}{3}×\frac{2}{4}= \frac{24}{12}=2$$$$b) \frac{16}{2}÷\frac{6}{3}=> \frac{16}{2}×\frac{3}{6}= \frac{36}{12}=3$$$$c) \frac{3}{4}÷\frac{5}{2}=> \frac{3}{4}×\frac{2}{5}= \frac{6}{20} = \frac{3}{10}\ (simplifiée)$$Simplifier une fraction c’est la rendre plus simple, on doit diviser le numérateur et le dénominateur par un même nombre (qui n’est pas 1).
$$Exemple: \frac{8}{12}\ simplifiée\ par\ 4\ est\ égale\ à\ \frac{2}{3}$$,
car 8÷4=2 et 12÷4=3. Le nombre par lequel on va diviser le numérateur et dénominateur doit être le plus nombre qui puisse diviserr les deux à la fois, ce nombre s’appelle: “Plus Grand Commun Diviseur” (PGCD). Voir: Les Plus Grands Diviseurs Communs
Quand la fraction ne peut plus être simplifier, on dit que la fraction est irréductible.
Partagez cet article sur: