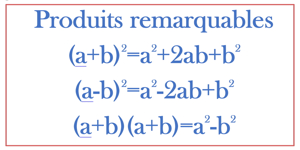Pour réussir à bien faire des calculs, il faut savoir les règles nécessaire dans chaque cas, par exemple, quand il y a des exposants, des additions et des multiplications, des parenthèses et d’autres éléments impliqués, il y a une règle qui explique comment faire.
Ces règles de calcul seront utiles pour tous les prochains cours et les classes supérieures.
Vous pouvez lire graduellement jusqu’à la fin ou encore tapez votre doigt sur le titre en bleu qui vous intéresse.
La priorité des parenthèses
La règle des signes
La priorité des opérations
La priorité des parenthèses
S’il y a des parenthèses dans une suite de calculs, on doit effectuer les calculs entre les parenthèses, en commençant par les parenthèses les plus intérieures.
Exemple: => nous allons effectuer d’abord ceux qui sont à l’intérieur des parenthèses.
A= 4 + 5 – 3 + (6 – 4 + 1)
A= 4 + 5 – 3 + 3
A= 9
B= 6 + 4 + (7 + 3 – (2 + 4) +1)
B= 6 + 4 + (7 + 3 – 6 +1)
B= 6 + 4 + 5
B= 15
Exercices, Mathématiques Nouvelles page 12 # 3, 4
- Calculez :
A= 28,2 – (9 + 11,7)
A= 28,2 – 20,7
A= 7,5
B= 120,8 – (11,4 – 7,9)
B= 120,8 – 3,5
B= 117,3
C= (7,8 – 4,5) x (11,2 – 3,4)
C= 3,3 × 7.8
C= 25,74
D= 15 x (0 + 2,2)
D= 15 × 2,2
D= 33
E= (15 + 22) x 0,7)
E= 37 × 0,7
E= 25,9
- Calculez :
A= (48 + 17) – 2
A= 65 – 2
A= 63
B= (48 – 17) + 2
B= 31 + 2
B= 33
C= 48 + (17 – 2)
C= 48 + 15
C= 63
D= 48 – ( 17 – 2)
D= 48 – 15
D= 33
La règle des signes
Quand on a deux mêmes signes, on fait une addition (ex: -2-3= -5 et +4+6= +10).
Pour deux signes contraires, on fait une soustraction et le résultat porte le signe du plus grand nombre (-8+5= -3 et +6-2= +4).
Il n’est pas néccessaire d’écrire le signe + au commencement d’un nombre ou d’une expression (ex: 6+8 = 14).
Priorité des opérations
Si dans une suite d’opération, il n y pas de parenthèses, les multiplications et les divisions doivent s’effectuer d’abord, et ensuite les additions et les soustractions.
S’il y a seulement des multiplications et des divisions, on doit les effectuer de la gauche vers la droite.
Exemple:
A= 3 + 5 × 4 – 7
A= 3 + 20 – 7
A= 23 – 7
A= 16
B= 6 – 2 × 8 + 12 ÷ 3 + 5 + 4
B= 6 – 16 + 4 + 5 + 4
B= 6 – 16 + 4 + 5 + 4
B= 19 – 16
B= 3
Exercices Mathématiques Nouvelles page 13 # 7, 8, 9
- Dans les calculs suivants, les parenthèses sont effacées. Remplace-les aux bons endroits de façon que les égalités soient vraies.
a) 2 + 5 × 3 = 21
a) (2 + 5) × 3 = 21
b) 8 – 5 + 2 = 5
b) (8 – 5) + 2 = 5
c) 15 × 6 – 4 = 86
c) (15 6) – 4 = 86
d) 15 x 6 – 4 = 30
d) 15 x (6 – 4) = 30
e) 2 × 2 + 2 × 2 = 16
e) 2 × (2 + 2) × 2 = 16
f) 2 × 2 + 2 × 2 = 12
f) 2 × (2 + (2 × 2)) = 12
g) 12 ÷ 3 + 3 = 2
g) 12 ÷ (3 + 3) = 2
h) 1000 ÷ 100 × 10 = 1
h) 1000 ÷ (100 × 10) = 1
- Même question (c’est-à-dire ajoute les parenthèses aux bons endroits de façon que les égalités soient vraies).
a) 25 × 4 – 2 + 2 × 5 = 108
a) (25 × 4) – 2 + (2 × 5) = 108
b) 20 – 1 ÷ 2 + 4 = 23,5
b) 20 – (1 ÷ 2) + 4 = 23,5
c) 16 ÷ 2 ÷ 2 ÷ 2 × 16 = 3,2
c) (16 ÷ 2) ÷ 2 ÷ 2 × 1,6 = 3,2
d) 13 + 13 + 13 ÷ 3 = 13
d) (13 + 13 + 13) ÷ 3 = 13
e) 18 × 13 – 2 × 5 – 23 = 31
e) 18 × (13 – 2 × 5) – 23 = 31
Exercices, Mathématiques Nouvelles page 13
- Calculez:
a) 9 × 16 ÷ 12 + 7 × 15 ÷ 21 + 26 × 35 ÷ 14 a) 144 ÷ 12 + 105 ÷ 21 + 910 ÷ 14 a) 12 + 5 + 65 a) 82
Partagez cet article sur: